Les normales
On peut lire, dans des textes sur les séries temporelles, des affirmations assez confuses sur la non-stationnarité des séries temporelles. On a l'impression que, dès qu'il y a quelque chose de non-stationnaire, il faut et suffit de différencier la série (avec quel pas, d'ailleurs ?) pour revenir au cadre ARMA.
On donne ici trois exemples très différents de séries temporelles non-stationnaires. Il s'agit de donner une intuition de la différence entre tendance stochastique et tendance déterministe, ces deux types de non-stationnarité appelant des traitements différents.
Le troisième exemple est une non-stationnarité plus complexe, qu'on ne peut pas faire rentrer dans le cadre ARMA défini par Box et Jenkins.
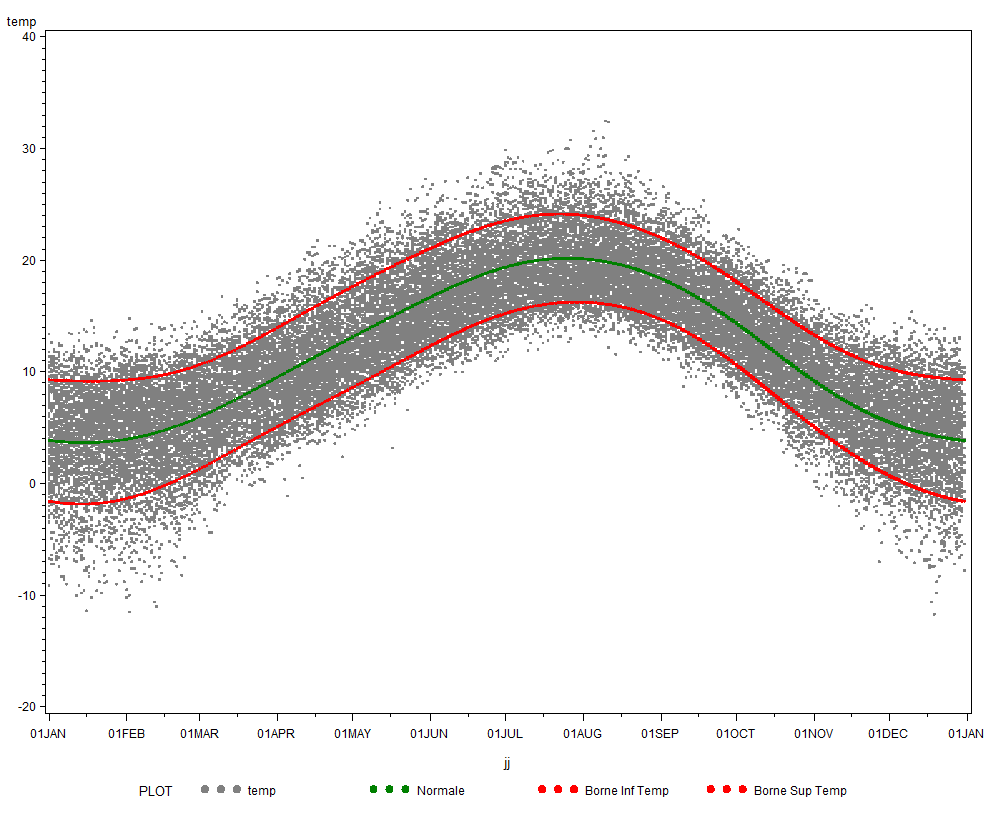
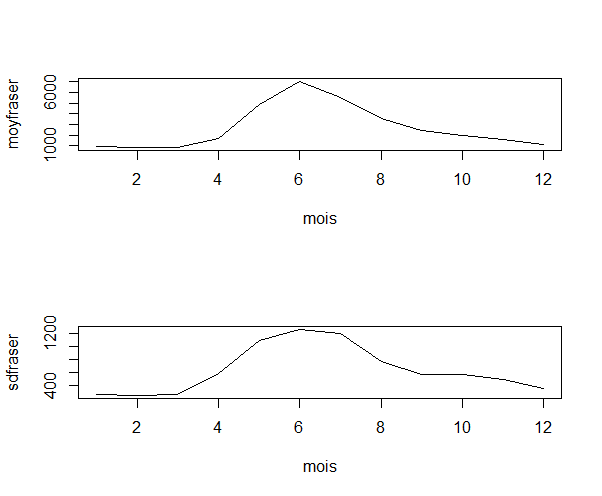
Par expérience, et les statistiques le confirment, la température varie au cours de l'année, aussi bien par sa moyenne que par sa variance. On peut le voir sur le graphique ci-dessous. Cette variation en moyenne et variance est très prévisible, la même d'une année à l'autre (au réchauffement climatique près), et peut être estimée par une régression.

Par ailleurs, autour de cette saisonnalité, il y a des écarts, dus à des fluctuations météorologiques. Ces écarts durent un certain temps (comme le fut du canon), mais s'atténuent à la longue.
Cela se traduit dans la fonction d'autocorrélation des écarts normalisés à la moyenne, qui converge vers 0 après une ou deux dizaines de jours.
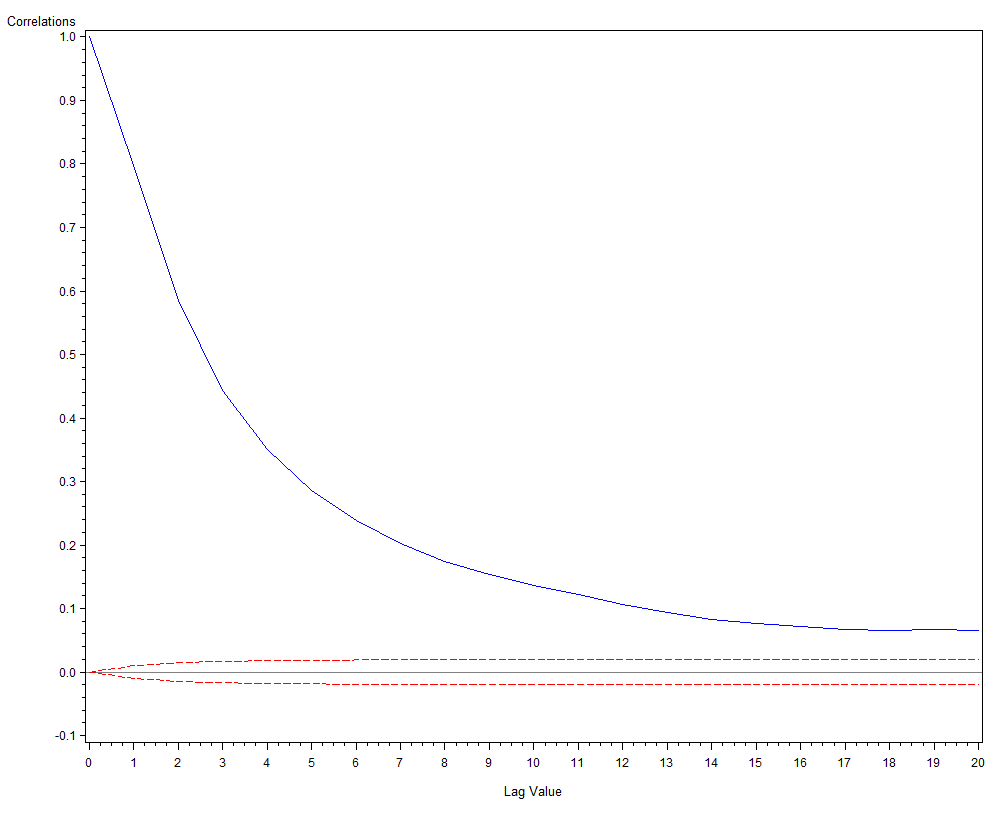
On parle dans ce cas de tendance déterministe : pour la température, la non-stationnarité peut etre supprimée par une régression, et les résidus de la régression ont une mémoire qui peut être utilisée pour construire un modèle ARMA.
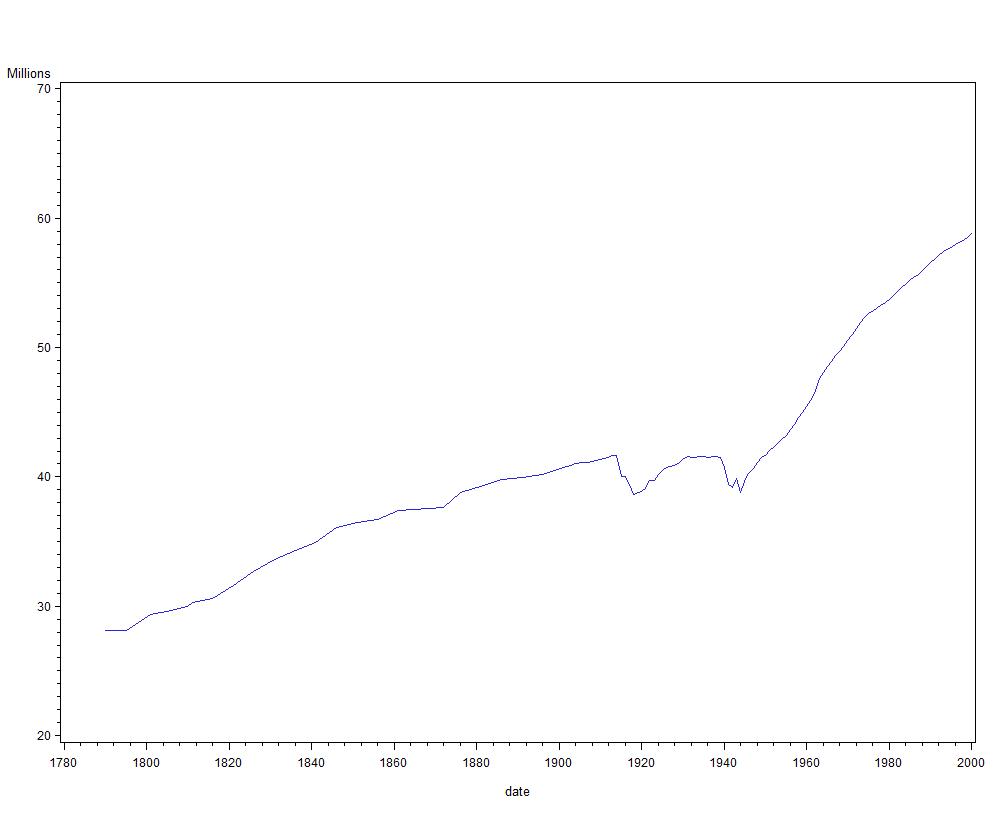
En ce qui concerne l'évolution d'une population, la première constatation est que cette progression est naturellement géométrique : le nombre d'enfants de chaque individu dépend peu de la taille de la population, dont l'évolution est donc géométrique.
Une autre constatation est qu'il n'y a pas d'atténuation des effets d'un écart à la moyenne. Ainsi, les morts et les non-nés des deux guerres mondiales ne réapparaissent pas, leurs non-enfants non plus.
Il est donc évident qu'il faut étudier les accroissements (en pourcentage) de la population, pas la population elle-même.
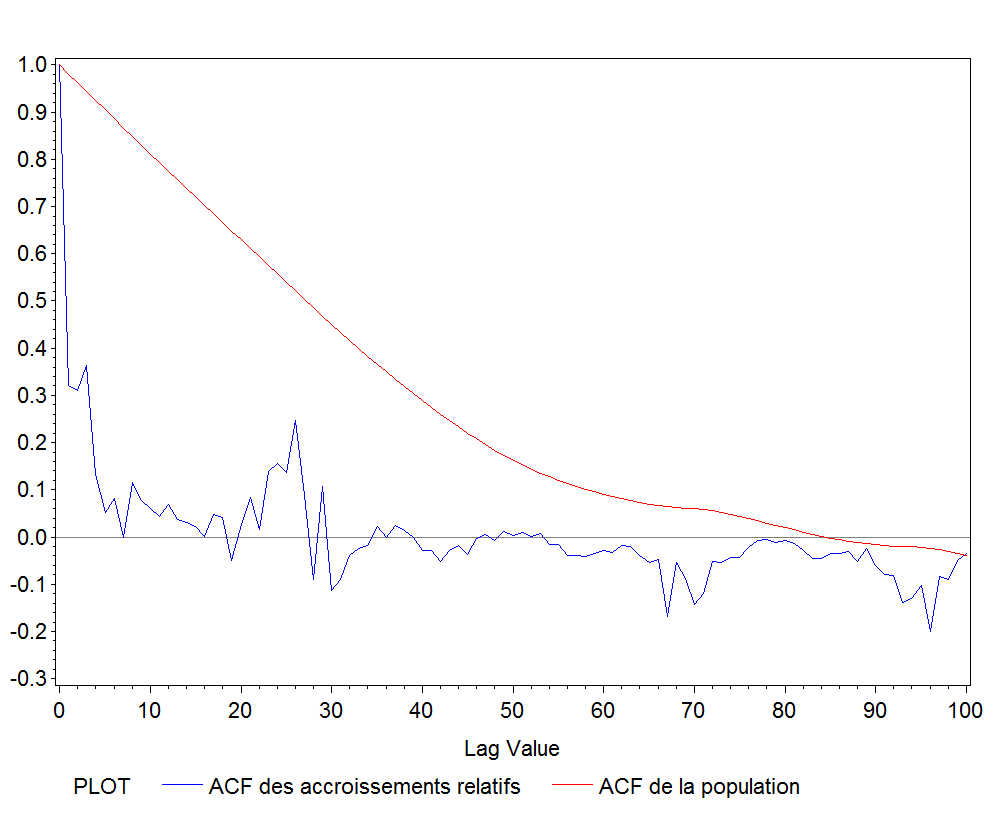
On voit ci-dessous deux fonctions d'autocorrélation: celle de la population, des des accroissements de la popualtion. Sans surprise, on constate que l'ACF de la population converge très lentement vers 0, les morts ne reviennent pas à la vie (la plupart du temps). Un modèle de série temporelle de la population devrait comprendre presque tout le passé, ce serait non seulement mathématiquement problématique, mais aussi pratiquement sans intérêt.
La fonction d'autocorrélation des accroissements est beaucoup plus intéressante. Elle se rapproche vite de 0. Elle est importante pendant les 2 ou 3 premières années, ce qui décrit une faible persistance des conditions poussant, à un moment donné, à une surnatalité. Surtout, elle redevient importante après une vingtaine d'années, ce qui est évidemment dù à l'arrivée à l'age de procréer des enfants du précédent baby-boom (ou l'inverse, mais je ne sais pas comment on dit en anglais).
On parle dans ce cas de tendance stochastique : pour les évolutions démographiques, la différentiation permet de supprimer la tendance et de revenir à une mémoire utilisable pour construire un modèle ARMA.
NB: La série très connue des prises de lynx est stationnaire, parce qu'elle oscille autour d'un point d'équilibre. Cet équilibre est déterminé par l'interaction avec la population de lièvre, qui est la nouritture des lynx. Ainsi, une grosse mortalité à un moment du passé décalerait un peu les oscillations, mais son effet dispaîtrait finalement. Le cas de la population française est différent, puisqu'elle n'oscille pas autour d'un point d'équilibre.
Ce que la différentiation permet de traiter, c'est le cas d'une série intégrée, autrement dit le cas d'une série où les aléas s'accumulent, où leur effet ne disparaît jamais.
Par ailleurs, une série intégrée est souvent non-stationnaire en moyenne (et toujours en variance). Néanmoins, il y a des cas assez simples où la non-stationnarité en moyenne et variance se traite à l'aide d'une régression.
Pour choisir entre ces deux méthodes, il est utile d'avoir une idée de «comment ça marche». Par ailleurs, ce choix peut aussi être fait à l'aide du test de Dickey-Fuller.
Ce qui est plus gênant, c'est que même les corrélations entre débits à des dates différentes dépendent du mois, comme le montre le graphique ci-dessous. Une raison possible est par exemple le régime nival : le débit d'une riviére de montagne dépend, au moment de la fonte des neiges, des précipitations de tout l'hiver, ce qui n'est pas le cas le reste de l'année.
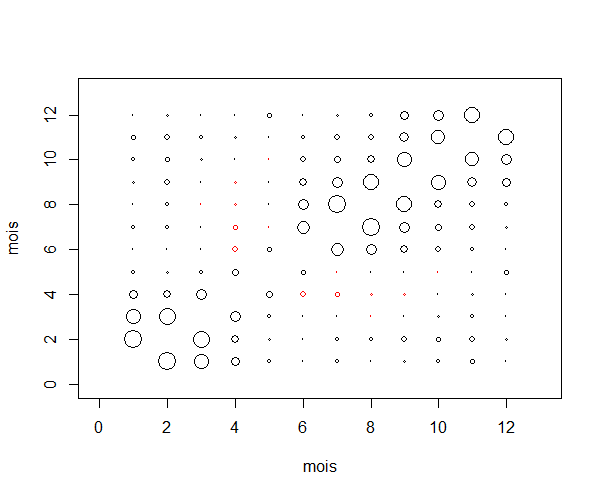
Il existe des modèles ARMA périodiques traitent ce genre de séries, mais dont l'utilisation reste encore ardue.